Fig 1: Clojure IDE: IntelliJ
The segue computation, twixt Python and Clojure, is this "volume of a tetrahedron based only on six edge lengths for input" algorithm handed down to me from the ancestors, and in my subculture fine tuned by one Gerald de Jong (of Elastic Interval Geometry fame) to natively output in what we call tetravolumes, i.e. when all edges are one, the thing is calibrated to return one (unit volume in this system).
Gerald shared his results on Synergetics-L which used to run in the Teleport domain. I brought the result to sci.math, coming under attack (by some guy named Chapman) for not getting my priorities straight. I have not gone back to sci.math with anything important (too frenetic!).
David Chako, Gerald, myself, and later Tom Ace, were all working on Quadrays at the time, which we also called Chakovian coordinates. I became aware of Darrel Jarmusch's parallel efforts somewhere in the course of this R&D.
Imagine a regular tetrahedron centered at O with four radial arms to its four vertexes. These are the unit vectors, at most three of which are needed, in linear combination, to span each quadrant. All IVM (= CCP) ball centers have positive integer or zero coordinates with origin O at (0, 0, 0, 0).
Quadrays may be used in combination with tetravolume measures to show all Waterman polyhedrons have whole number volume, as do all tetrahedrons with all four corners at IVM points (proof by Robert Gray, the original transcriber of Synergetics onto the Web).
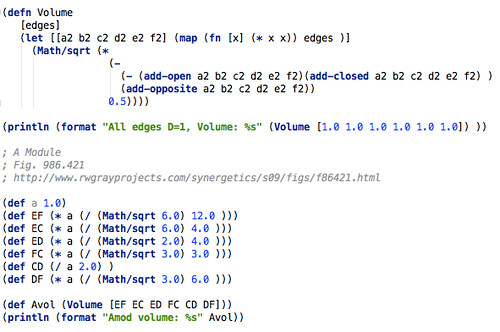
To use the Volume function (below), one gives the three edges from a common apex, call it O, meaning we input OA, OB, OC. The next three edges are the AB, BC, CA respectively, i.e. going around the base. The algorithm works with 2nd powers of these lengths, forming products of "open", "closed" and "opposite" sets of edges.
Fig 2: Call-out: the Volume function
In the above figure, the summary Volume computation is matched with a special case example, that of the A module, for output of:
All edges D=1, Volume: 1.0 Amod volume: 0.04166666666666668
The labeling in that case corresponds to some plane net in Synergetics. The unit volume tetrahedron fragments into 24 such modules, 12 left and 12 right (inside-outs of each other), and therefore each with a volume of 1/24 (same as B and T modules).
The Clojure program, just like the Python version, then goes on to compute other module volumes, including the E and S module volumes, from published plane nets, with the S / E volume ratio named "sFactor" in other computations relating to the Jitterbug Transformation (see CSN blog).
I recommend Wittgenstein's philosophical investigations, into mathematics especially, for those balking at the very notion of a unit volume tetrahedron, which may at first seem counter-intuitive, just as Clojure's LISP-like syntax may feel too alien (remote) at first.
Showing how the tetravolumes language game extents to the planar case, along with the payoff in terms of whole number volumes, may lower the student's skepticism level enough to where engaging in hands-on exercises with these concepts, using computer languages, does not seem a waste of time on some purely nonsensical activity.