"Cramming" is a term used by Global U students when feeling up against a deadline to produce in some way. In my case, we've just finished Session 8 of 10, adding to a 40 hour course on the Python computer language. That's just one of my gigs.
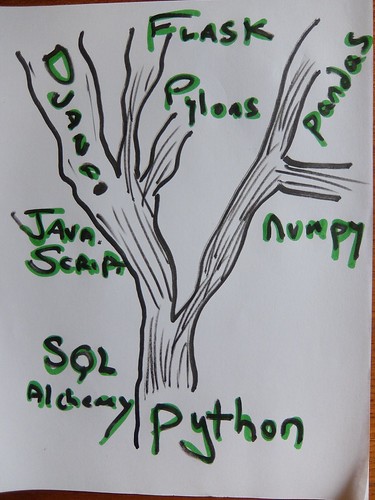
Once mastery of core Python (keywords, builtins, special names) has been achieved, we branch out in two more of the five dimensions: Standard Library and 3rd Party.
A fact of life in the high tech world is we're awash in toys but with little time to play with them, someone's idea of a joke perhaps.
Like, Python is cram packed with interesting little gizmos, feats of genius, and future generations inherit a goldmine of possibility.
We only have time to mine a little in our day. Mostly we're running from negative phenomena, many of them self inflicted. Humans are not on the side of humans. The movie Wonder Woman looks into this.
Heading up the Python tree, a first branch is into web development. Are we behind an HTTPS / HTTP server and if so, do we also need a database?
Web servers have become the way to share files. You don't even need a landing page for human eyeball browsers. Your clients are other computers and they're hungry for JSON, not HTML.
One of the most used web servers in this regard is the Jupyter Notebook server. Most researchers install it locally and serve themselves, from localhost:8888 or one of those. In this case, we do want HTML, but also a running kernel capable of interpreting language X, which might be Python, but could also be JavaScript or SQL.
Given the Python marathon, and all my recent victories around Synergetics, I'm content to post less to math-teach and more to the Python websites, regarding the explorations I've been undertaking with D. B. Koski.
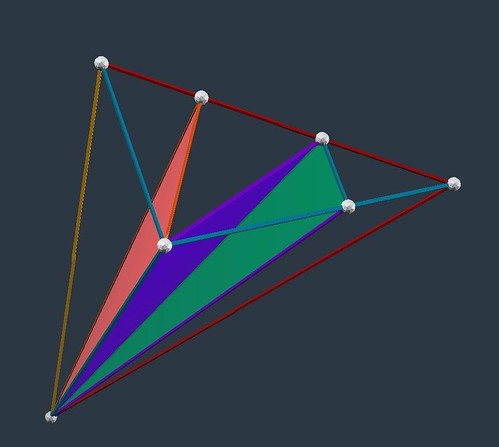
He takes the LCD triangles (spherical) of the 31 great circle Icosahedron, which relate to the 25 of the cuboctahedron, and turns them into plane nets about four modules: the E (each a 1/4 slice of the 30 rhombus 120 LCD triangle Rhombic Triacontahedron, radius 1); then: Fe, Fi, Fo, Fum (taking pronunciations from the fairy tale).
A shared edge of the Fe and Fi, which latter has E's volume "phi down" (phi^-3 scale factor), has a length we've taken to calling the S Factor, likewise the ratio of VE:Icosa both of Jitterbug fame, and of S-to E-mods (S/E): about 1.08.
The icosahedron embedded within the volume 4 octahedron, of edges 2, from whence the S modules are carved, has edges that same length? I hadn't tuned that in. I'll use Python as a kind of spreadsheet, or dataframe, to explore more in that direction.
In this way, I'm able to keep my fingers on a keyboard, composing with mathematical concepts, while staying in shape for my morning and evening seminars, not to mention the time in schools.
I'm a big believer in a varied diet, so I'm not painting the above regime as some frieze of the rest of my life. However, I think having coding and/or geometry as a frequent mental activity serves the same role as walking a mile a day or visiting the gym.
Use it or lose it right?
That's what the professors really mean when they say "publish or perish" as usually how we know you haven't lost it, are using it, is we get to peer review.
The S Factor should not be confused with S3, Fuller's published constant for volumetric conversion between a Cartesian XYZ cube of edges sqrt(2) i.e. sqrt(2)^3, and an IVM-based cube with the same edges, but embracing a different "unit of volume", in this case a 2-edged Tetrahedron.
Thanks to a theorem, the IVM volume (tetravolume) is of said tetrahedron-embracing cube is 3, giving 3 / sqrt(2)^3 as our S3 "currency conversion" ratio of about 1.060660171779821 (as computed in Python), see Table 986.209.
Once mastery of core Python (keywords, builtins, special names) has been achieved, we branch out in two more of the five dimensions: Standard Library and 3rd Party.
A fact of life in the high tech world is we're awash in toys but with little time to play with them, someone's idea of a joke perhaps.
Like, Python is cram packed with interesting little gizmos, feats of genius, and future generations inherit a goldmine of possibility.
We only have time to mine a little in our day. Mostly we're running from negative phenomena, many of them self inflicted. Humans are not on the side of humans. The movie Wonder Woman looks into this.
Heading up the Python tree, a first branch is into web development. Are we behind an HTTPS / HTTP server and if so, do we also need a database?
Web servers have become the way to share files. You don't even need a landing page for human eyeball browsers. Your clients are other computers and they're hungry for JSON, not HTML.
One of the most used web servers in this regard is the Jupyter Notebook server. Most researchers install it locally and serve themselves, from localhost:8888 or one of those. In this case, we do want HTML, but also a running kernel capable of interpreting language X, which might be Python, but could also be JavaScript or SQL.
Given the Python marathon, and all my recent victories around Synergetics, I'm content to post less to math-teach and more to the Python websites, regarding the explorations I've been undertaking with D. B. Koski.
He takes the LCD triangles (spherical) of the 31 great circle Icosahedron, which relate to the 25 of the cuboctahedron, and turns them into plane nets about four modules: the E (each a 1/4 slice of the 30 rhombus 120 LCD triangle Rhombic Triacontahedron, radius 1); then: Fe, Fi, Fo, Fum (taking pronunciations from the fairy tale).
A shared edge of the Fe and Fi, which latter has E's volume "phi down" (phi^-3 scale factor), has a length we've taken to calling the S Factor, likewise the ratio of VE:Icosa both of Jitterbug fame, and of S-to E-mods (S/E): about 1.08.
The icosahedron embedded within the volume 4 octahedron, of edges 2, from whence the S modules are carved, has edges that same length? I hadn't tuned that in. I'll use Python as a kind of spreadsheet, or dataframe, to explore more in that direction.
In this way, I'm able to keep my fingers on a keyboard, composing with mathematical concepts, while staying in shape for my morning and evening seminars, not to mention the time in schools.
I'm a big believer in a varied diet, so I'm not painting the above regime as some frieze of the rest of my life. However, I think having coding and/or geometry as a frequent mental activity serves the same role as walking a mile a day or visiting the gym.
Use it or lose it right?
That's what the professors really mean when they say "publish or perish" as usually how we know you haven't lost it, are using it, is we get to peer review.
The S Factor should not be confused with S3, Fuller's published constant for volumetric conversion between a Cartesian XYZ cube of edges sqrt(2) i.e. sqrt(2)^3, and an IVM-based cube with the same edges, but embracing a different "unit of volume", in this case a 2-edged Tetrahedron.
Thanks to a theorem, the IVM volume (tetravolume) is of said tetrahedron-embracing cube is 3, giving 3 / sqrt(2)^3 as our S3 "currency conversion" ratio of about 1.060660171779821 (as computed in Python), see Table 986.209.
982.32 The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(2^3), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428.An interesting discovery of Koski's regarding S3 is it's also the ratio of SuperRT / VE, i.e. the classic D-edged VE of tetravolume 20, in a Jitterbug relationship with D-edged Icosahedron, when multiplied by S3, gives the volume of the RT formed by said Icosa and its dual, the Pentagonal Dodecahedron (we call that SuperRT, "phi up" from the 120 E-modules RT).
:: left to right: Fum, Fo, Fi, Fe ::